Árvore AVL

Árvore AVL
Tipo	Árvore
Ano	1962
Inventado por	Georgy Adelson-Velsky e Yevgeniy Landis
Complexidade de Tempo em Notação big O

Árvore AVL é uma árvore binária de busca balanceada^[2], ou seja, uma árvore balanceada (árvore completa) são as árvores que minimizam o número de comparações efetuadas no pior caso para uma busca com chaves de probabilidades de ocorrências idênticas. Contudo, para garantir essa propriedade em aplicações dinâmicas, é preciso reconstruir a árvore para seu estado ideal a cada operação sobre seus nós (inclusão ou exclusão), para ser alcançado um custo de algoritmo com o tempo de pesquisa tendendo a $O(\log n)$ .

As operações de busca, inserção e remoção de elementos possuem complexidade $O(\log n)$ (no qual $n$ é o número de elementos da árvore), que são aplicados a árvore de busca binária.

O nome AVL vem de seus criadores soviéticos Adelson Velsky e Landis, e sua primeira referência encontra-se no documento "Algoritmos para organização da informação" de 1962 ^[3].

Nessa estrutura de dados cada elemento é chamado de nó. Cada nó armazena uma chave e dois ponteiros, uma para a subárvore esquerda e outro para a subárvore direita.

No presente artigo serão apresentados: os conceitos básicos, incluindo uma proposta de estrutura; apresentação das operações busca, inserção e remoção, todas com complexidade $O(\log n)$ .

História

Esta estrutura foi criada em 1962 pelos soviéticos Adelson Velsky e Landis que a criaram para que fosse possível inserir e buscar um elemento em tempo c.log (n) operações, onde n é o número de elementos contido na árvore. Tal estrutura foi a primeira árvore binária balanceada criada^[4].

Conceitos básicos

Definição

Uma árvore binária T é denominada AVL quando, para qualquer nó de T, as alturas de suas duas subárvores, esquerda e direita, diferem em módulo de até uma unidade.^[5]

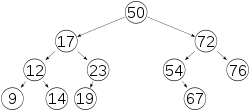
Pela definição fica estabelecido que todos os nós de uma árvore AVL devem respeitar a seguinte propriedade:

|h_d(u) - h_e(u)| ≤ 1, onde h_d(u) é a altura da subárvore direita do nó u e h_e(u) é a altura da subárvore esquerda do nó u.

O valor h_d(u) - h_e(u) é denominado fator de balanço do nó. Quando um nó possui fator de balanço com valor -1, 0 ou 1 então o mesmo é um nó regulado. Todos os nós de uma árvore AVL são regulados, caso contrário a árvore não é AVL.

Estrutura

Proposta de estrutura dos nós de uma árvore AVL básica, com chave do tipo inteiro:

tipo No_AVL = registro
    chave: inteiro;
    fb: inteiro; // Fator de Balanço
    esq: ^No_AVL;  // aponta subárvore esquerda
    dir: ^No_AVL;  // aponta subárvore direita
fim;

O campo chave armazena o valor da chave. Os campos esq e dir são ponteiros para as subárvores esquerda e direita, respectivamente. O campo fb armazena o fator de balanço.

Definição da estrutura da árvore:

tipo Arvore_AVL = registro
    raiz: ^No_AVL;
    // definição de outros campos de interesse
fim;

Balanceamento

Toda árvore AVL é balanceada, isto é, sua altura é O(log n).^[5]

A vantagem do balanceamento é possibilitar que a busca seja de complexidade O(log n). Entretanto, as operações de inserção e remoção devem possuir custo similar. No caso da árvore AVL, a inserção e remoção têm custo O(log n).

Por definição, todos os nós da AVL devem ter fb = -1, 0 ou 1.

Para garantir essa propriedade, a cada inserção ou remoção o fator de balanço deve ser atualizado a partir do pai do nó inserido até a raiz da árvore. Na inserção basta encontrar o primeiro nó desregulado (fb= -2 ou fb= 2), aplicar o operação de rotação necessária, não havendo necessidade de verificar os demais nós. Na remoção a verificação deverá prosseguir até a raiz, podendo requerer mais de uma rotação.

Uma árvore AVL sempre terá um tamanho menor que^[6]:

$\log _{\varphi }({\sqrt {5}}(n+2))-2={\frac {\log _{2}({\sqrt {5}}(n+2))}{\log _{2}(\varphi )}}-2=\log _{\varphi }(2)\cdot \log _{2}({\sqrt {5}}(n+2))-2\approx 1.44\log _{2}(n+2)-0.328$

Onde n é o número de elementos da árvore e $\varphi$ é a proporção áurea.

Complexidade

A árvore AVL tem complexidade $O(\log n)$ para todas operações e ocupa espaço n, onde n é o número de nós da árvore.

Complexidade da árvore AVL em notação O
	Média	Pior caso
Espaço	$O(n)$	$O(n)$
Busca	$O(\log n)$	$O(\log n)$
Inserção	$O(\log n)$	$O(\log n)$
Deleção	$O(\log n)$	$O(\log n)$

Operações

Busca

A busca é a mesma utilizada em árvore binária de busca.

A busca pela chave de valor K inicia sempre pelo nó raiz da árvore.

Seja pt_u um ponteiro para o nó u sendo verificado. Caso o pt_u seja nulo então a busca não foi bem sucedida (K não está na árvore ou árvore vazia). Verificar se a chave K igual pt_u->chave (valor chave armazenado no nó u), então a busca foi bem sucedida. Caso contrário, se K < pt_u->chave então a busca segue pela subárvore esquerda; caso contrário, a busca segue pela subárvore direita.

Algoritmo de busca

busca_AVL(@pt_u:^no_AVL, K:inteiro):logico;
inicio
se  pt_u é NULO então retornar Falso;
se K = pt_u->chave então retornar Verdadeiro;
senão se K < pt_u->chave então
         retornar busca_AVL(u->esq, K);
      senão retornar busca_AVL(u->dir, K);
fim.

Exemplo de algoritmo de busca em Java.

// O método de procura numa AVL é semelhante ao busca binária de uma árvore binária de busca comum.
public BSTNode<T> search(T element) {
    return search(element, this.root);
}

// Método auxiliar à recursão.
private BSTNode<T> search(T element, BSTNode<T> node) {
    if (element == null || node.isEmpty()) {
        return new BSTNode<T>();
    }
    
    if (node.isEmpty() || node.getData().equals(element)) {
        return node;
    } else if (node.getData().compareTo(element) > 0) {
        return search(element, node.getLeft());
    } else {
        return search(element, node.getRight());
    }
}

Inserção

Para inserir um novo nó de valor K em uma árvore AVL é necessária uma busca por K nesta mesma árvore. Após a busca o local correto para a inserção do nó K será em uma subárvore vazia de uma folha da árvore. Depois de inserido o nó, a altura do nó pai e de todos os nós acima deve ser atualizada. Em seguida o algoritmo de rotação simples ou dupla deve ser acionado para o primeiro nó pai desregulado.

Algoritmo recursivo

inserir_AVL(@p:^no_AVL, K:inteiro, @mudou_h:logico):logico;
var aux: logico; // variável local auxiliar;
inicio
se  p = NULO então
    inicio // não achou chave, inserir neste local
    p := novo(no_AVL);  // aloca novo nó dinamicamente, diretamente na subárvore do nó pai
    p^.chave := K;
    p^.esq := NULO;
    p^.dir := NULO;
    mudou_h := Verdadeiro; // sinalizar que a altura da subárvore mudou 1 unidade
    retornar Verdadeiro;
    fim;
se K < p^.chave então // inserir recursivamente na subárvore esquerda
    se inserir_AVL(p^.esq, K, mudou_h) então // ocorreu inserção na subárvore esquerda
        inicio
        se mudou_h então
            inicio  // mudou altura da subárvore esquerda de p
            p^.fb := p^.fb - 1; // fator de balanço decrementa 1 unidade
            caso p^.fb
                -2: p := rotacao_direita(p); mudou_h := Falso;
                 0: mudou_h := Falso; // não mudou a altura da subárvore de raiz p
            //   -1: mudou_h := Verdadeiro; // desnecessário pois mudou_h já é Verdadeiro
            fim
        retornar Verdadeiro;
        fim
senão
    se K > p^.chave então  // ocorreu inserção na subárvore direita
        se inserir_AVL(p^.dir, K, mudou_h) então // ocorreu inserção
        inicio
        se mudou_h então
            inicio  // mudou altura da subárvore esquerda de p
            p^.fb := p^.fb + 1; // fator de balanço incrementa 1 unidade
            caso p^.fb
                 2: p := rotacao_esquerda(p); mudou_h := Falso;
                 0: mudou_h := Falso; // não mudou a altura da subárvore de raiz p
            //   1: mudou_h := Verdadeiro; // desnecessário pois mudou_h já é Verdadeiro
            fim
        retornar Verdadeiro;
        fim
retornar Falso;
fim.

Os parâmetros p e mudou_h são passados por referência. O ponteiro p aponta para o nó atual. O parâmetro mudou_h é do tipo lógico e informa ao chamador se a subárvore apontada por p mudou sua altura.

Como identificar mudança de altura?

Considerar que o nó p é raiz da subárvore T_p e houve inserção em uma de suas subárvores.

Caso a subárvore T_p tenha mudado de altura, decrementar fb (inserção na subárvore esquerda) ou incrementar fb (inserção na subárvore direita).

Caso 1: Ao inserir um nó folha, a subárvore T_p passa de altura 0 para altura 1, então T_p mudou de altura.

Caso 2: fb=0 antes da inserção foi alterado para 1 ou -1, então a subárvore T_p mudou de altura.

Caso 3: fb=1 ou -1 antes da inserção, passou a ter valor 0, então a subárvore T_p não mudou de altura.

Caso 4: O fb passou a ter valor -2 ou 2 após a inserção, então há necessidade de aplicação de alguma operação de rotação. Após a rotação, a subárvore T_p terá a mesma altura anterior à inserção.

Exemplo de algoritmo de inserção em Java

/* Por definição, a árvore AVL é uma árvore binária de busca (BST).
*  Por este motivo utiliza-se aqui a mesma definição (classe) de Nós que uma BST simples.
*/
public void insert(T element) {
    insertAux(element);
    BSTNode<T> node = search(element); // Pode-se utilizar o mesmo search exemplificado acima.
    rebalanceUp(node);
}

private void insertAux(T element) {
    if (element == null) return;
    insert(element, this.root);
}

private void insert(T element, BSTNode<T> node) {
    if (node.isEmpty()) {
        node.setData(element);
        node.setLeft(new BSTNode<T>());
        node.setRight(new BSTNode<T>());
        node.getLeft().setParent(node);
        node.getRight().setParent(node);
    } else {
        if (node.getData().compareTo(element) < 0) {
            insert(element, node.getRight());
        } else if (node.getData().compareTo(element) > 0) {
            insert(element, node.getLeft());
        }
    }
}

Algoritmos de complemento à inserção e/ou algoritmos para identificar desbalanceamento em Java

protected void rebalanceUp(BSTNode<T> node) {
    if (node == null || node.isEmpty()) return;
    rebalance(node);
    if (node.getParent() != null) {
        rebalanceUp(node.getParent());
    }
}

protected int calculateBalance(BSTNode<T> node) {
    if (node == null || node.isEmpty()) return 0;
    return height(node.getRight()) - height(node.getLeft()); 
}

protected void rebalance(BSTNode<T> node) {
    int balanceOfNode = calculateBalance(node);
    
    if (balanceOfNode < -1) {
        if (calculateBalance(node.getLeft()) > 0) {
            leftRotation(node.getLeft());
        }
        rightRotation(node);
    } else if (balanceOfNode > 1) {
        if (calculateBalance(node.getRight()) < 0) {
            rightRotation(node.getRight());
        }
        leftRotation(node);
    }
}

Rotação para Direita e para Esquerda em Java

protected void leftRotation(BSTNode<T> no) {
	BTNode<T> noDireito = no.getRight();

	no.setRight(noDireito.getLeft());

	noDireito.getLeft().setParent(no);
	noDireito.setLeft(no);
	noDireito.setParent(no.getParent());
	no.setParent(noDireito);

	if (no != this.getRoot()) {
		if (noDireito.getParent().getLeft() == no) {
			noDireito.getParent().setLeft(noDireito);
		} else {
			noDireito.getParent().setRight(noDireito);
		}
	} else {
			this.root = (BSTNode<T>) noDireito;
	}
}

protected void rightRotation(BSTNode<T> no) {
	BTNode<T> noEsquerdo = no.getLeft();

	no.setLeft(noEsquerdo.getRight());

	noEsquerdo.getRight().setParent(no);
	noEsquerdo.setRight(no);
	noEsquerdo.setParent(no.getParent());
	no.setParent(noEsquerdo);

	if (no != this.getRoot()) {
		if (noEsquerdo.getParent().getLeft() == no) {
			noEsquerdo.getParent().setLeft(noEsquerdo);
		} else {
			noEsquerdo.getParent().setRight(noEsquerdo);
		}
	} else {
		this.root = (BSTNode<T>) noEsquerdo;
	}
}

Remoção

O primeiro passo para remover uma chave K consiste em realizar uma busca binária a partir do nó raiz. Caso a busca encerre em uma subárvore vazia, então a chave não está na árvore e a remoção não pode ser realizada. Caso a busca encerre em um nó u o nó que contenha a chave então a remoção poderá ser realizada da seguinte forma:

Caso 1: O nó u é uma folha da árvore, apenas exclui-lo.

Caso 2: O nó u tem apenas uma subárvore, necessariamente composta de um nó folha, basta apontar o nó pai de u para a única subárvore e excluir o nó u.

Caso 3: O nó u tem duas subárvores: localizar o nó v predecessor ou sucessor de K, que sempre será um nó folha ou possuirá apenas uma subárvore; copiar a chave de v para o nó u; excluir o nó v a partir da respectiva subárvore de u.

O último passo consiste em verificar a desregulagem de todos nós a partir do pai do nó excluído até o nó raiz da árvore. Aplicar rotação simples ou dupla em cada nó desregulado.

Algoritmo recursivo

remover_AVL(@p:^no_AVL, K:inteiro, @mudou_h:logico):logico;
var q:^No_AVL;  // ponteiro auxiliar para nó
inicio
se  p = NULO então
    retornar Falso; // não achou a chave K a ser removida
se K < p^.chave então // remover recursivamente na subárvore esquerda
    se remover_AVL(p^.esq, K, mudou_h) então // ocorreu remoção na subárvore esquerda
        inicio
        se mudou_h então
            inicio  // mudou altura da subárvore esquerda de p
            p^.fb := p^.fb + 1; // fator de balanço incrementa 1 unidade
            caso p^.fb
                2:  p := rotacao_esquerda(p);
                    se (p->fb=1) então mudou_h := Falso;
                1: mudou_h := Falso; // não mudou a altura da subárvore de raiz p
               // 0: mudou_h := Verdadeiro; // desnecessário pois mudou_h já é Verdadeiro
            fim
        retornar Verdadeiro;
        fim
senão
    se K > p^.chave então
        se remover_AVL(p^.dir, K, mudou_h) então // ocorreu remoção na s.a. direita
            inicio
            se mudou_h então
                inicio  // mudou altura da subárvore direita de p
                p^.fb := p^.fb - 1; // fator de balanço decrementa 1 unidade
                caso p^.fb
                    -2: p := rotacao_direita(p);
                        se (p->fb = -1) então mudou_h := Falso;
                    -1: mudou_h := Falso; // não mudou a altura da subárvore de raiz p
                //   0: mudou_h := Verdadeiro; // desnecessário pois mudou_h já é Verdadeiro
                fim
            retornar Verdadeiro;
            fim
    senão inicio
            se K = p^.chave então // achou a chave K
                inicio
                se p^.esq=Nulo e p^.dir=Nulo então
                    inicio // nó folha
                    delete p;
                    p := Nulo; // Aterra a subárvore respectiva do nó pai
                    mudou_h := Verdadeiro;
                    fim
                senão se p^.esq<>Nulo e p^.dir<>Nulo então
                        inicio  // nó tem duas subárvores
                        q := Predecessor(p);  // retorna nó com chave predecessora
                        p^.chave := q^.chave;
                        remover(p^.esq,p^.chave,mudou_h);
                        fim
                      senão inicio // tem apenas uma subárvore
                            se p^.esq<>Nulo então
                                inicio
                                p^.chave := p^.esq^.chave;
                                delete p^.esq;
                                p^.esq := Nulo;
                                fim
                            senão   inicio
                                    p^.chave := p^.dir^.chave;
                                    delete(p^.dir);
                                    p^.dir := Nulo;
                                    fim;
                            mudou_h = Verdadeiro;
                            fim;
                retornar Verdadeiro;
                fim
            fim
retornar Falso;
fim;

Predecessor(u:^No_AVL):^No_AVL // retorna nó contendo chave predecessora
inicio
u = u^.esq; // aponta para a raiz da subárvore esquerda
enquanto(u^.dir<>Nulo) faça  // procura a maior chave da subárvore esquerda
    u := u^.dir;
retornar u;  // retorna o predecessor
fim;

Exemplo de algoritmo de remoção em Java

public void remover(int valor) {
		removerAVL(this.raiz, valor);
	}

	private void removerAVL(No atual, int valor) {
		if (atual != null) {

			if (atual.getChave() > valor) {
				removerAVL(atual.getEsquerda(), valor);

			} else if (atual.getChave() < valor) {
				removerAVL(atual.getDireita(), valor);

			} else if (atual.getChave() == valor) {
				removerNoEncontrado(atual);
			}
		}
	}

	private void removerNoEncontrado(No noARemover) {
		No no;

		if (noARemover.getEsquerda() == null || noARemover.getDireita() == null) {

			if (noARemover.getPai() == null) {
				this.raiz = null;
				noARemover = null;
				return;
			}
			no = noARemover;

		} else {
			no = sucessor(noARemover);
			noARemover.setChave(no.getChave());
		}

		No no2;
		if (no.getEsquerda() != null) {
			no2 = no.getEsquerda();
		} else {
			no2 = no.getDireita();
		}

		if (no2 != null) {
			no2.setPai(no.getPai());
		}

		if (no.getPai() == null) {
			this.raiz = no2;
		} else {
			if (no == no.getPai().getEsquerda()) {
				no.getPai().setEsquerda(no2);
			} else {
				no.getPai().setDireita(no2);
			}
			verificarBalanceamento(no.getPai());
		}
		no = null;
	}

^[7] Algoritmos auxilares na remoção

public No sucessor(No no) {
		if (no.getDireita() != null) {
			No noDireita = no.getDireita();
			while (noDireita.getEsquerda() != null) {
				noDireita = noDireita.getEsquerda();
			}
			return noDireita;
		} else {
			No noPai = no.getPai();
			while (noPai != null && no == noPai.getDireita()) {
				no = noPai;
				noPai = no.getPai();
			}
			return noPai;
		}
	}
	public void verificarBalanceamento(No atual) {
		setBalanceamento(atual);
		int balanceamento = atual.getBalanceamento();

		if (balanceamento == -2) {

			if (altura(atual.getEsquerda().getEsquerda()) >= altura(atual.getEsquerda().getDireita())) {
				atual = rotacaoDireita(atual);

			} else {
				atual = duplaRotacaoEsquerdaDireita(atual);
			}

		} else if (balanceamento == 2) {

			if (altura(atual.getDireita().getDireita()) >= altura(atual.getDireita().getEsquerda())) {
				atual = rotacaoEsquerda(atual);

			} else {
				atual = duplaRotacaoDireitaEsquerda(atual);
			}
		}

		if (atual.getPai() != null) {
			verificarBalanceamento(atual.getPai());
		} else {
			this.raiz = atual;
		}
	}
	
	public No rotacaoEsquerda(No inicial) {

		No direita = inicial.getDireita();
		direita.setPai(inicial.getPai());

		inicial.setDireita(direita.getEsquerda());

		if (inicial.getDireita() != null) {
			inicial.getDireita().setPai(inicial);
		}

		direita.setEsquerda(inicial);
		inicial.setPai(direita);

		if (direita.getPai() != null) {

			if (direita.getPai().getDireita() == inicial) {
				direita.getPai().setDireita(direita);
			
			} else if (direita.getPai().getEsquerda() == inicial) {
				direita.getPai().setEsquerda(direita);
			}
		}

		setBalanceamento(inicial);
		setBalanceamento(direita);

		return direita;
	}

	public No rotacaoDireita(No inicial) {

		No esquerda = inicial.getEsquerda();
		esquerda.setPai(inicial.getPai());

		inicial.setEsquerda(esquerda.getDireita());

		if (inicial.getEsquerda() != null) {
			inicial.getEsquerda().setPai(inicial);
		}

		esquerda.setDireita(inicial);
		inicial.setPai(esquerda);

		if (esquerda.getPai() != null) {

			if (esquerda.getPai().getDireita() == inicial) {
				esquerda.getPai().setDireita(esquerda);
			
			} else if (esquerda.getPai().getEsquerda() == inicial) {
				esquerda.getPai().setEsquerda(esquerda);
			}
		}

		setBalanceamento(inicial);
		setBalanceamento(esquerda);

		return esquerda;
	}

	public No duplaRotacaoEsquerdaDireita(No inicial) {
		inicial.setEsquerda(rotacaoEsquerda(inicial.getEsquerda()));
		return rotacaoDireita(inicial);
	}

	public No duplaRotacaoDireitaEsquerda(No inicial) {
		inicial.setDireita(rotacaoDireita(inicial.getDireita()));
		return rotacaoEsquerda(inicial);
	}
	
	private void setBalanceamento(No no) {
		no.setBalanceamento(altura(no.getDireita()) - altura(no.getEsquerda()));
	}
	
	private int altura(No atual) {
		if (atual == null) {
			return -1;
		}

		if (atual.getEsquerda() == null && atual.getDireita() == null) {
			return 0;
		
		} else if (atual.getEsquerda() == null) {
			return 1 + altura(atual.getDireita());
		
		} else if (atual.getDireita() == null) {
			return 1 + altura(atual.getEsquerda());
		
		} else {
			return 1 + Math.max(altura(atual.getEsquerda()), altura(atual.getDireita()));
		}
	}

^[7]

Como identificar mudança de altura na remoção ?

Considerar que o nó p é raiz da subárvore T_p e houve remoção em uma de suas subárvores.

Caso a subárvore T_p tenha mudado de altura, incrementar fb (remoção na subárvore esquerda) ou decrementar fb (remoção na subárvore direita).

Caso 1: Ao remover um nó folha, a subárvore T_p passa de altura 1 para altura 0, então T_p mudou de altura.

Caso 2: fb=0 antes da remoção foi alterado para 1 (remoção à esquerda) ou -1 (remoção à direita), então a subárvore T_p não mudou de altura.

Caso 3: fb=1 ou -1 antes da remoção à direita e à esquerda, respectivamente, passando a ter valor 0, então a subárvore T_p mudou de altura.

Caso 4: fb passou a ter valor -2 ou 2 após a remoção, então houve necessidade de aplicação de rotação. Após a rotação dupla T_p muda de altura, exceto quando u=0 (antes da remoção- caso não relatado na literatura).

Rotação

A operação básica em uma árvore AVL geralmente envolve os mesmos algoritmos de uma árvore de busca binária desbalanceada. A rotação na árvore AVL ocorre devido ao seu desbalanceamento, uma rotação simples ocorre quando um nó está desbalanceado e seu filho estiver no mesmo sentido da inclinação, formando uma linha reta. Uma rotação-dupla ocorre quando um nó estiver desbalanceado e seu filho estiver inclinado no sentido inverso ao pai, formando um "joelho".

Para garantirmos as propriedades da árvore AVL rotações devem ser feitas conforme necessário após operações de remoção ou inserção. Seja P o nó pai, FE o filho da esquerda de P e FD o filho da direita de P podemos definir 4 tipos diferentes de rotação:

Rotação simples à direita

Deve ser efetuada quando a diferença das alturas h dos filhos de P é igual a 2 e a diferença das alturas h dos filhos de FE é igual a 1. O nó FE deve tornar o novo pai e o nó P deve se tornar o filho da direita de FE. Segue pseudocódigo:

Seja Y o filho à esquerda de X
Torne o filho à direita de Y o filho à esquerda de X.
Torne X o filho à direita de Y

Rotação à esquerda

Deve ser efetuada quando a diferença das alturas h dos filhos de P é igual a -2 e a diferença das alturas h dos filhos de FD é igual a -1. O nó FD deve tornar o novo pai e o nó P deve se tornar o filho da esquerda de FD. Segue pseudocódigo:

Seja Y o filho à direita de X
Torne o filho à esquerda de Y o filho à direita de X.
Torne X filho à esquerda de Y
Rotação simples a esquerda

Rotação dupla à direita

Deve ser efetuada quando a diferença das alturas h dos filhos de P é igual a 2 e a diferença das alturas h dos filhos de FE é igual a -1. Nesse caso devemos aplicar uma rotação à esquerda no nó FE e, em seguida, uma rotação à direita no nó P.

Deve ser observado que as 3 possíveis combinações de alturas da subárvores T₂ e T₃ constam da figura (h, h-1; h, h; e h-1, h), implicando em nos respectivos balanços do nó u (0/0/-1) e do nó p (1/0/0).

Rotação dupla à esquerda

Deve ser efetuada quando a diferença das alturas h dos filhos de P é igual a -2 e a diferença das alturas h dos filhos de FD é igual a 1. Nesse caso devemos aplicar uma rotação à direita no nó FD e, em seguida, uma rotação à esquerda no nó P.

Rotação dupla à esquerda

Algoritmo de rotação à direita

rotaçaoDireita(p:NoAVL):@NoAVL;
inicio
var u,v:@NoAVL;
u := p^.esq;
se u^.fb > 0 então
    inicio // rotação dupla, conforme figura Caso 1.2
     v := u^.dir;
     u^.dir := v^.esq;
     p^.esq := c^.dir;
     v^.esq := u;
     v^.dir := p;
     caso v->fb
        -1: u^.fb := 0; p^.fb := 1;
        0: u^.fb := 0; p^.fb := 0;
        1: u^.fb := -1; p^.fb := 0;
     v^.fb := 0;
     retornar v;
     fim;
// rotaçao simples, conforme figura Caso 1.1
p^.esq := u^.dir;
u^.dir := p;
se u^.fb < 0 então
    inicio
    u^.fb := 0;
    p^.fb := 0;
    fim;
senão inicio  // ocorre apenas na remoção - não relatado na literatura
      u^.fb := 1;
      p^.fb := -1;
      fim;
retornar u;
fim;

Cabe ressaltar, apesar de não estar relatado na literatura, que na remoção poderá ocorre a situação na qual u^.fb=0. Neste caso deverá ser aplicada rotação simples e o fator de balanço dos nós u e p serão respectivamente 1 e -1.

Rotação à esquerda

Caso o fator de balanço do nó p tenha valor +2, então haverá necessidade de aplicar rotação simples ou dupla à esquerda.

Para identificar se qual rotação aplicar, bastará analisar o fator de balanço do nó u, raiz da subárvore direita do nó p.

Rotação simples à esquerda

Caso o fator de balanço do nó u seja +1, então deverá ser aplicada uma rotação simples à esquerda. A figura a seguir mostra a configuração da árvore antes e depois da rotação.

Rotação dupla à esquerda

Caso o fator de balanço do nó u seja -1, então deverá ser aplicada uma rotação dupla à esquerda. A figura a seguir mostra a configuração da árvore antes e depois da rotação.

Aplicações

A árvore AVL é muito útil, pois executa as operações de inserção, busca e remoção em tempo O(log n). Comparado-a com a árvore rubro-negra, a AVL é mais rápido nas aplicações que fazem uma quantidade excessiva de buscas, porém esta estrutura é um pouco mais lenta para inserção e remoção. Isso se deve ao fato de as árvores AVL serem mais rigidamente balanceadas.

Dicionários

Árvore AVL pode ser usada para formar um dicionário de uma linguagem ou de programas, como os opcodes de um assembler ou um interpretador.

Geometria Computacional

Árvore AVL pode ser usada também na geometria computacional por ser uma estrutura muito rápida. Sem uma estrutura com complexidade O(log n) alguns algoritmos da geometria computacional poderiam demorar dias para serem executados.

Conjuntos

Árvore AVL podem ser empregadas na implementação de conjuntos, principalmente aqueles cujas chave não são números inteiros.

A complexidade das principais operações de conjuntos usando árvore AVL:

Inserir - O(log n);
Remover - O(log n);
Pertence - O(log n);
União - O(n.log n);
Interseção - O(n.log n).

Referências

↑ ^a ^b ^c ^d ^e ^f Eric Alexander. «AVL Trees»
↑ Cormen, Thomas H. (2009). Introduction to Algorithms,. Massachusetts Institute of Technology: MIT Press. 333 páginas
↑ Adel'son-Vel'skiĭ, G. M.; Landis, E. M. (1962), "An algorithm for organization of information", Doklady Akademii Nauk SSSR, 146: 263–266.
↑ Kent, Allen; Williams, James G. (1993), Encyclopedia of Computer Science and Technology: Volume 28 - Supplement 13: AerosPate Applications of Artificial Intelligence to Tree Structures, CRC Press, p. 373, ISBN 9780824722814.
↑ ^a ^b Swarcfiter, Jayme Luiz (1994). Estruturas de dados e seus algoritmos. Rio de Janeiro, Brasil: LTC. 130 páginas
↑ Knuth, Donald E. (2000). Sorting and searching (2. ed., 6. printing, newly updated and rev. ed.). Boston [u.a.]: Addison-Wesley. p. 460. ISBN 0-201-89685-0.
↑ ^a ^b «Implementação de Árvore AVL em Java, baseada em www.blackbam.at/blackbams-blog/2012/05/04/avl-tree-implementation-in-java/». Gist (em inglês). Consultado em 24 de agosto de 2017

Bibliografia

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Third Edition. MIT Press, 2009. p. 333. ISBN 978-0-262-53305-8.
Adelson-Velskii, G.; E. M. Landis (1962). "An algorithm for the organization of information". Proceedings of the USSR Academy of Sciences 146: 263–266. (Russian) English translation by Myron J. Ricci in Soviet Math. Doklady, 3:1259–1263, 1962.
Jayme Luiz Szwarcfiter, Lilian Markenzon. Estruturas de Dados e Seus Algoritmos, 2010. p. 130-144. ISBN 85-215-1014-9.

Ver também

O Commons possui uma categoria com imagens e outros ficheiros sobre Árvore AVL

Árvore binária de busca
Árvore rubro-negra
Árvore B
Árvore Patricia
«Inserção, remoção e alteração em árvores AVL». www.site.uottawa.ca
Notação O

[wiscurl-1] ↑ ^a ^b ^c ^d ^e ^f Eric Alexander. «AVL Trees»

[2] Cormen, Thomas H. (2009). Introduction to Algorithms,. Massachusetts Institute of Technology: MIT Press. 333 páginas

[3] Adel'son-Vel'skiĭ, G. M.; Landis, E. M. (1962), "An algorithm for organization of information", Doklady Akademii Nauk SSSR, 146: 263–266.

[4] Kent, Allen; Williams, James G. (1993), Encyclopedia of Computer Science and Technology: Volume 28 - Supplement 13: AerosPate Applications of Artificial Intelligence to Tree Structures, CRC Press, p. 373, ISBN 9780824722814.

[:0-5] Swarcfiter, Jayme Luiz (1994). Estruturas de dados e seus algoritmos. Rio de Janeiro, Brasil: LTC. 130 páginas

[6] Knuth, Donald E. (2000). Sorting and searching (2. ed., 6. printing, newly updated and rev. ed.). Boston [u.a.]: Addison-Wesley. p. 460. ISBN 0-201-89685-0.

[gist.github.com-7] «Implementação de Árvore AVL em Java, baseada em www.blackbam.at/blackbams-blog/2012/05/04/avl-tree-implementation-in-java/». Gist (em inglês). Consultado em 24 de agosto de 2017

[1]

[2]

[3]

[4]

[5]

[6]

[7]

v d e Estrutura de dados
Tipos	Coleção Container
Abstrato	Vetor associativo Multimap Lista Pilha Fila Deque Fila de prioridade Fila de prioridade duplamente terminada Conjunto Multiset Disjoint-set
Arrays	Bit array Buffer circular Array dinâmico Tabela hash Matriz esparsa
Vinculada	Lista associativa Lista ligada Skiplist Lista ligada XOR
Árvore	Árvore B Árvore binária de busca Árvore AA Árvore AVL Árvore rubro-negra Árvore binária de busca balanceada Árvore splay Heap Heap binária Heap binomial Heap de Fibonacci Árvores R Árvore R* Árvore R+ Árvore R de Hilbert Trie Árvores de Merkle
Grafos	Diagramas de decisão binária Grafos acíclicos dirigidos Autômato finito determinístico acíclico
Lista de estruturas de dados

v d e Árvores (estrutura de dados)
Árvores de busca (conjuntos dinâmicos/vetores associativos)	2-3 2-3-4 AA (a,b) AVL B B+ B* Binária Intervalo Rubro-negra Scapegoat Splay T Treap
Heaps	Binária Binomial Brodal Fibonacci Esquerdista Van Emde Boas
Tries	PATRICIA Sufixo Ternária
Árvores de particionamento de dados espaciais	BK BSP Hilbert R k-d M Métrica Octree Quaternária R R+ R* Segmentos VP
Outras árvores	Fenwick K-ária Merkle Hiperbólica